This inconsistent ranking is unlikely to occur for an individual. If Duncan Thurly, a well-known hypothetical person, prefers chocolate ice cream to glazed donuts and also prefers glazed donuts to carrot cake, then he undoubtedly also prefers chocolate ice cream to carrot cake.

A committee of three or more people, in contrast, might express a preference for chocolate ice cream to glazed donuts and also glazed donuts to carrot cake, but then indicate a preference of carrot cake to chocolate ice cream.

The problem with this potential voting paradox is that the group of voters might not only fail to reach a decision, but the decision reached need not be efficient.

A Subcommittee of Three

The Voting Paradox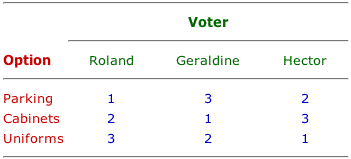

The relative ranking of preferences of the three alternatives by the three members is presented in the exhibit at the right. Roland's first choice is the parking lot, his second is display cabinets, and his last is employee uniforms. Geraldine's preference ranking is display cabinets, followed by employee uniforms, then the parking lot. At the top of Hector's ranking is employee uniforms, with the parking lot his second choice, and display cabinets at the bottom of his list.

Putting it to a Vote

• Parking Lot and Display Cabinets: First, let's see how this subcommittee ranks resurfacing the parking lot versus new display cabinets. Roland prefers the parking lot over the display cabinets. Geraldine prefers display cabinets over the parking lot. The deciding vote is then cast by Hector, who also prefers the parking lot project over buying new display cabinets. As such, the subcommittee ranks the parking lot over the display cabinets by a vote of 2 to 1.


• Display Cabinets and Employee Uniforms: Now let's compare the subcommittee's relative ranking of new display cabinets versus new uniforms for the employees. Roland prefers the display cabinets over employee uniforms. Geraldine also prefers display cabinets over employee uniforms. Hector is the only member who prefers employee uniforms over display cabinets. As such, the subcommittee ranks the purchase of display cabinets to the purchase of employee uniforms by a vote of 2 to 1.

• Parking Lot and Employee Uniforms: Roland prefers the parking lot over employee uniforms. Geraldine, however, prefers employee uniforms over the parking lot. Once again, the deciding vote is cast by Hector. In this case, Hector prefers employee uniforms over the parking lot. The subcommittee ranks the new employee uniforms over resurfacing the parking lot by a vote of 2 to 1.

Are these three members crazy? Are they irrational?

Not at all. They are merely exhibiting the voting paradox.

What it Means

• Decision Order: First, the order in which decisions are made affects the outcome. If our Shoe Museum Committee has enough funds only for two of the three projects, then the order of the vote, AND ONLY THE ORDER OF THE VOTE, determines which of the three projects will be undertaken. Any two of the three projects can be selected over the third, depending on the order of the vote. As the chairman of the Shoe Museum Committee, Lance can easily obtain whatever result he wants merely by setting the agenda.


• Efficiency: Second, decisions made by the committee are not necessarily efficient. There is no mechanism to indicate which project provides the greatest satisfaction from available resources. Perhaps resurfacing the parking lot is the most efficiency use of resources. Perhaps it is new display cabinets. Or perhaps it is new employee uniforms. Whichever alternative might be most efficient is irrelevant to whatever choice is ultimately made by the subcommittee.

Other Voting Problems

• Median Voter: This voting principle, one that is well known by politicians, is that the median voter determines the outcome of an election. The median voter is the one with an equal number of voters on either side of the vote. As such, the vote cast by THE median voter is the deciding vote. However, this median voter's preference might not generate the best, that is, efficient, result.


• Logrolling: This is the process in which voters trade votes to ensure the passage of two separate issues neither one of which would receive a majority on its own. This is commonly done in legislative bodies. It's also something that can lead to an inefficient use of resources.


• Rational Voter Apathy: Voters can be considered apathetic because they rational choose to not be informed (rational ignorance) and not to participate in the process (rational abstention). In each case votes (and nonvoters) undertake actions that maximize utility, but such actions mean their preferences are not adequately included in the political process.