
|
|
REGULATION: Government rules or laws that control the activities of businesses and consumers. The motivation for regulation is that businesses are inclined to do things that are harmful to the public--actions which need to be prevented or otherwise controlled. Regulation is essentially an extension of government's authority to protect one member of society from another. It tends to take one of two forms--(1) industry regulation that's intended to prevent firms from gaining and abusing excessive market control and (2) social regulation that seeks to protect consumers for problems caused by pollution, unsafe products, and the lack of information (market failure).
Visit the GLOSS*arama
|
|


|

|
                           CONSUMPTION FUNCTION: A mathematical relation between consumption and income by the household sector. The consumption function can be stated as an equation, usually a simple linear equation, or as a diagram designated as the consumption line. This function captures the consumption-income relation that forms one of the key building blocks for Keynesian economics. The two key parameters of the consumption function are the intercept term, which indicates autonomous consumption, and the slope, which is the marginal propensity to consume and indicates induced consumption. Aggregate expenditures used in Keynesian economics are derived by adding investment, government purchases, and net exports to the consumption function. The consumption function is the starting point in the Keynesian economics analysis of equilibrium output determination. It captures the fundamental psychological law put forth by John Maynard Keynes that consumption expenditures by the household sector depend on income and than only a portion of additional income is used for consumption.This function is presented either as a mathematical equation, most often as a simple linear equation, or as the graphical consumption line. In either form, consumption is measured by consumption expenditures and income is measured as disposable income, national income, or occasionally gross domestic product. The primary purpose of the consumption function the basic consumption-income relation for the household sector, which is the foundation of the aggregate expenditures line used in Keynesian economics. The consumption function makes it easy to divide consumption into two basic types. Autonomous consumption is the intercept term. Induced consumption is the slope. Of no small importance, the slope of the consumption function is also the marginal propensity to consume (MPC). First, The EquationThe consumption function can represented in a general form as:where: C is consumption expenditures, Y is income (national or disposable), and f is the notation for a generic, unspecified functional form.Depending on the analysis, the actual functional form of the equation can be linear, with a constant slope, or curvilinear, with a changing slope. The most common form is linear, such as the one presented here: where: C is consumption expenditures, Y is income (national or disposable), a is the intercept, and b is the slope.The two key parameters that characterize the consumption function are slope and intercept. - Slope: The slope of the consumption function (b) measures the change in consumption resulting from a change in income. If income changes by $1, then consumption changes by $b. This slope is generally assumed and empirically documented to be greater than zero, but less than one (0 < b < 1). It is conceptually identified as induced consumption and the marginal propensity to consume (MPC).
- Intercept: The intercept of the consumption function (a) measures the amount of consumption undertaken if income is zero. If income is zero, then consumption is $a. The intercept is generally assumed and empirically documented to be positive (0 < a). It is conceptually identified as autonomous consumption.
Then, The Graph| Consumption Line | 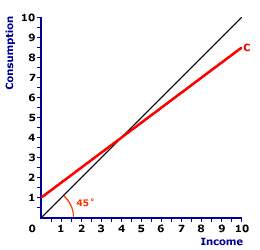
|
The consumption function is also commonly presented as a diagram or consumption line, such as the one presented in the exhibit to the right. This red line, labeled C in the exhibit is positively sloped, indicating that greater levels of income generate greater consumption expenditures by the household sector. The specific consumption function illustrated in this exhibit is:For reference, a black 45-degree line is also presented in this exhibit. Because this line has a slope of one, it indicates the relative slope of the consumption line. The two primary characteristics of the consumption function--slope and intercept--also can be identified with the consumption line. - Slope: The slope of the consumption line presented here is positive, but less than one. In this case the slope is equal to 0.75. Click the [Slope] button to highlight.
- Intercept: The consumption line intersects the vertical axis at a positive value of $1 trillion. Click the [Intercept] button to highlight.
And Other FactorsThe consumption function captures the relation between consumption and income. However, income is not the only factor influencing consumption. where: C is consumption expenditures, Y is income (national or disposable), and now OF is specified as other factors affecting consumption. These other factors, officially referred to as consumption expenditures determinants, include a range of influences. Some of the more notable consumption determinants are consumer confidence, interest rates, and wealth.Consumer confidence is the general optimism or pessimism the household sector has about the state of the economy. More optimism means more consumption. Interest rates affect the cost of borrowing the funds used to purchase durable goods. Higher interest rates mean less consumption. Wealth is the financial and physical assets owned by the household sector. More financial wealth means more consumption, while more physical assets mean less consumption. These determinants cause consumption expenditures to change even though income does not change. Or another way of stating this, determinants cause consumption expenditures to change at every level of income. For a linear consumption function, this change is reflected by a change in the intercept term (a). For a consumption line, the change is seen as an upward or downward shift.

Recommended Citation:CONSUMPTION FUNCTION, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2024. [Accessed: July 26, 2024].
Check Out These Related Terms... | | | | | | | | | | | | |
Or For A Little Background... | | | | | | | | | | |
And For Further Study... | | | | | | | | | | | | | | |
Search Again?
Back to the WEB*pedia
|



|

|
PINK FADFLY
[What's This?]
Today, you are likely to spend a great deal of time at a dollar discount store hoping to buy either a how-to book on fine dining or a coffee cup commemorating the first day of winter. Be on the lookout for letters from the Internal Revenue Service.
Your Complete Scope
This isn't me! What am I?
|

|
|
Okun's Law posits that the unemployment rate increases by 1% for every 2% gap between real GDP and full-employment real GDP.
|

|
|
"Old age isn't so bad when you consider the alternative. " -- Cato, Roman orator
|

|
CBOE
Chicago Board Options Exchange
|

|
|
Tell us what you think about AmosWEB. Like what you see? Have suggestions for improvements? Let us know. Click the User Feedback link.
User Feedback
|


|


