
|
|
WHOLESALE PRICE INDEX: An index of the prices paid by retail stores for the products they would ultimately resell to consumers. The Wholesale Price Index, abbreviated WPI, was the forerunner of the modern Producer Price Index (PPI). The WPI was first published in 1902, and was one of the more important economic indicators available to policy makers until it was replaced by the PPI in 1978. The change to Producer Price Index in 1978 reflected, as much as a name change, a change in focus of this index away from the limited wholesaler-to-retailer transaction to encompass all stages of production. While the WPI is no longer available, the family of producer price indexes provides a close counterpart in the Finished Goods Price Index.
Visit the GLOSS*arama
|
|


|

|
                           MONOPOLISTIC COMPETITION: A market structure characterized by a large number of small firms, similar but not identical products sold by all firms, relative freedom of entry into and exit out of the industry, and extensive knowledge of prices and technology. This is one of four basic market structures. The other three are perfect competition, monopoly, and oligopoly. Monopolistic competition approximates most of the characteristics of perfect competition, but falls short of reaching the ideal benchmark that IS perfect competition. It is the best approximation of perfect competition that the real world offers. Monopolistic competition is a market structure characterized by a large number of relatively small firms. While the goods produced by the firms in the industry are similar, slight differences often exist. As such, firms operating in monopolistic competition are extremely competitive but each has a small degree of market control.In effect, monopolistic competition is something of a hybrid between perfect competition and monopoly. Comparable to perfect competition, monopolistic competition contains a large number of extremely competitive firms. However, comparable to monopoly, each firm has market control and faces a negatively-sloped demand curve',500,400)">demand curve. The real world is widely populated by monopolistic competition. Perhaps half of the economy's total production comes from monopolistically competitive firms. The best examples of monopolistic competition come from retail trade, including restaurants, clothing stores, and convenience stores. CharacteristicsThe four characteristics of monopolistic competition are: (1) large number of small firms, (2) similar, but not identical products, (3) relatively good, but not perfect resource mobility, and (4) extensive, but not perfect knowledge.- Large Number of Small Firms: A monopolistically competitive industry contains a large number of small firms, each of which is relatively small compared to the overall size of the market. This ensures that all firms are relatively competitive with very little market control over price or quantity. In particular, each firm has hundreds or even thousands of potential competitors.
- Similar Products: Each firm in a monopolistically competitive market sells a similar, but not absolutely identical, product. The goods sold by the firms are close substitutes for one another, just not perfect substitutes. Most important, each good satisfies the same basic want or need. The goods might have subtle but actual physical differences or they might only be perceived different by the buyers. Whatever the reason, buyers treat the goods as similar, but different.
- Relative Resource Mobility: Monopolistically competitive firms are relatively free to enter and exit an industry. There might be a few restrictions, but not many. These firms are not "perfectly" mobile as with perfect competition, but they are largely unrestricted by government rules and regulations, start-up cost, or other substantial barriers to entry.
- Extensive Knowledge: In monopolistic competition, buyers do not know everything, but they have relatively complete information about alternative prices. They also have relatively complete information about product differences, brand names, etc. Each seller also has relatively complete information about production techniques and the prices charged by their competitors.
Product DifferentiationThe goods produced by firms operating in a monopolistically competitive market are subject to product differentiation. The goods are essentially the same, but they have slight differences.Product differentiation is usually achieved in one of three ways: (1) physical differences, (2) perceived differences, and (3) support services. - Physical Differences: In some cases the product of one firm is physically different form the product of other firms. One good is chocolate, the other is vanilla. One good uses plastic, the other aluminum.
- Perceived Differences: In other cases goods are only perceived to be different by the buyers, even though no physical differences exist. Such differences are often created by brand names, where the only difference is the packaging.
- Support Services: In still other cases, products that are physically identical and perceived to be identical are differentiated by support services. Even though the products purchased are identical, one retail store might offer "service with a smile," while another provides express checkout.
Product differentiation is the primary reason that each firm operating in a monopolistically competitive market is able to create a little monopoly all to itself.Demand and RevenueDemand Curve,
Monopolistic Competition | 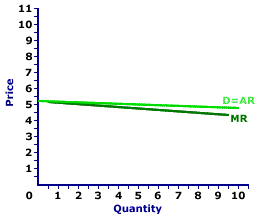 |
The four characteristics of monopolistic competition mean that a monopolistically competitive firm faces a relatively elastic, but not perfectly elastic, demand curve, such as the one displayed in the exhibit to the right. Each firm in a monopolistically competitive market can sell a wide range of output within a relatively narrow range of prices.Demand is relatively elastic in monopolistic competition because each firm faces competition from a large number of very, very close substitutes. However, demand is not perfectly elastic (as in perfect competition) because the output of each firm is slightly different from that of other firms. Monopolistically competitive goods are close substitutes, but not perfect substitutes. In the exhibit to the right, the monopolistically competitive firm can sell up to 10 units of output within the range of $5.50 to $6.50. Should the price go higher than $6.50, the quantity demanded drops to zero. A monopolistically competitive firm is a price maker, with some degree of control over price. Once again, unlike perfect competition, a monopolistically competitive firm has the ability to raise or lower the price a little, not much, but a little. And like monopoly, the price received by a monopolistically competitive firm (which is also the firm's average revenue) is greater than its marginal revenue. In the exhibit to the right, the marginal revenue curve (MR) lies below the demand/average revenue curve (D = AR). While marginal revenue is less than price, because demand is relatively elastic, the difference tends to be relatively small. For example, 5 units of output correspond to a $5 price. The marginal revenue for the fifth unit is $4.80, less than price, but not by much. Short-Run ProductionShort-Run Production,
Monopolistic Competition | 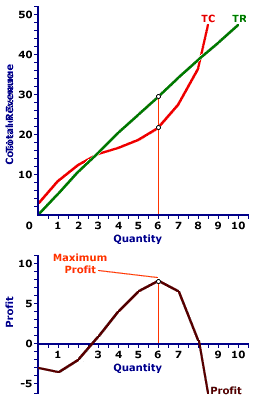 |
The analysis of short-run production by a monopolistically competitive firm provides insight into market supply. The key assumption is that a monopolistically competitive firm, like any other firm, is motivated by profit maximization. The firm chooses to produce the quantity of output that generates the highest possible level of profit, given price, market demand, cost conditions, production technology, etc.The short-run production decision for monopolistic competition can be illustrated using the exhibit to the right. The top panel indicates the two sides of the profit decision--revenue and cost. The slightly curved green line is total revenue. Because price depends on quantity, the total revenue curve is not a straight line. The curved red line is total cost. The difference between total revenue and total cost is profit, which is illustrated in the lower panel as the brown line. A firm maximizes profit by selecting the quantity of output that generates the greatest gap between the total revenue line and the total cost line in the upper panel, or at the peak of the profit curve in the lower panel. In this example, the profit maximizing output quantity is 6. Any other level of production generates less profit. Long-Run ProductionIn the long run, with all inputs variable, a monopolistically competitive industry reaches equilibrium at an output that generates economies of scale or increasing returns to scale. At this level of output, the negatively-sloped demand curve is tangent to the negatively-sloped segment of the long run-average cost curve.This is achieved through a two-fold adjustment process. - The first of the folds is entry and exit of firms into and out of the industry. This ensures that firms earn zero economic profit and that price is equal to average cost.
- The second of the folds is the pursuit of profit maximization by each firm in the industry. This ensures that firms produce the quantity of output that equates marginal revenue with short-run and long-run marginal cost.
Because a monopolistically competitive firm has some market control and faces a negatively-sloped demand curve, the end result of this long-run adjustment is two equilibrium conditions:| MR = MC = LRMC | | P = AR = ATC = LRAC |
With marginal revenue equal to marginal cost, each firm is maximizing profit and has no reason to adjust the quantity of output or factory size. With price equal to average cost, each firm in the industry is earning only a normal profit. Economic profit is zero and there are no economic losses, meaning no firm is inclined to enter or exit the industry.These conditions are satisfied separately. However, because price is not equal to marginal revenue, the two equations are not equal (unlike perfect competition). This further means that monopolistic competition does NOT achieve long-run equilibrium at the minimum efficient scale of production. Real World (In)EfficiencyA monopolistically competitive firm generally produces less output and charges a higher price than would be the case for a perfectly competitive industry. In particular, the price charged by a monopolistically competitive firm is greater than its marginal cost.The inequality of price and marginal cost violates the key condition for efficiency. Resources are NOT being used to generate the highest possible level of satisfaction. The reason for this inefficiency is found with market control. Because a monopolistically competitive firm has control over a small slice of the market, it faces a negatively-sloped demand curve and price is greater than marginal revenue, which is set equal to marginal cost when maximizing profit. While monopolistic competition is technically inefficient, it tends to be less inefficient than other market structures, especially monopoly. Even though price is greater than marginal revenue (and thus marginal cost), because the demand curve is relatively elastic, the difference is often relatively small. For example, a monopoly that charges a $100 price while incurring a marginal cost of $20 creates a serious inefficiency problem. In contrast, the inefficiency created by a monopolistically competitive firm that charges a $50 price while incurring a marginal cost of $49.95 is substantially less. The closer marginal revenue is to price, the closer a monopolistically competitive firm comes to allocating resources according to the efficiency benchmark established by perfect competition. In the grand scheme of economic problems, the inefficiency created by monopolistic competition seldom warrants much attention... and deservedly so. The Other Three Market Structures| Market Structure Continuum |  |
Monopolistic competition is one of four common market structures. The other three are: perfect competition, monopoly, and oligopoly. The exhibit to the right illustrates how these four market structures form a continuum based on the relative degree of market control and the number of competitors in the market. In the middle of the market structure continuum, near the left end, is monopolistic competition, characterized by numerous competitors and limited market control.- Perfect Competition: To the far left of the market structure continuum is perfect competition, characterized by a large number of relatively small competitors, each with no market control. Perfect competition is an idealized market structure that provides a benchmark for efficiency.
- Monopoly: To the far right of the market structure continuum is monopoly, characterized by a single competitor and extensive market control. Monopoly contains a single seller of a unique product with no close substitutes. The demand for monopoly output is THE market demand.
- Oligopoly: In the middle of the market structure continuum, residing closer to monopoly, is oligopoly, characterized by a small number of relatively large competitors, each with substantial market control. A substantial number of real world markets fit the characteristics of oligopoly.
On the surface, oligopoly and monopolistic competition seem quite different. Oligopoly contains a few large firms that dominate a market. Monopolistic competition contains a large number of small firms, each with some, but not a lot of market control. However, monopolistic competition and oligopoly are actually the heart and soul of the market structure continuum.There is no clear-cut, obvious dividing line between monopolistic competition and oligopoly. While a three-firm industry is most assuredly an oligopoly and a 3,000 firm industry is most likely monopolistic competition, an industry with 30 firms could be considered either oligopoly or monopolistic competition. For example, convenience stores in a large city are undoubtedly monopolistically competitive. However, convenience stores in a smaller town might very well be oligopoly.

Recommended Citation:MONOPOLISTIC COMPETITION, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2025. [Accessed: June 30, 2025].
Check Out These Related Terms... | | | |
Or For A Little Background... | | | | | | | | | | | | |
And For Further Study... | | | | | | | |
Related Websites (Will Open in New Window)... | | | |
Search Again?
Back to the WEB*pedia
|



|

|
YELLOW CHIPPEROON
[What's This?]
Today, you are likely to spend a great deal of time flipping through mail order catalogs looking to buy either income tax software or a how-to book on the art of negotiation. Be on the lookout for fairy dust that tastes like salt.
Your Complete Scope
This isn't me! What am I?
|

|
|
The New York Stock Exchange was established by a group of investors in New York City in 1817 under a buttonwood tree at the end of a little road named Wall Street.
|

|
|
"I learned about the strength you can get from a close family life. I learned to keep going, even in bad times. I learned not to despair, even when my world was falling apart. I learned that there are no free lunches. And I learned the value of hard work. " -- Lee Iacocca
|

|
DOL
Department of Labor
|

|
|
Tell us what you think about AmosWEB. Like what you see? Have suggestions for improvements? Let us know. Click the User Feedback link.
User Feedback
|


|


