
|
|
VALUE IN EXCHANGE: The ability to trade an item, especially money, for other goods and services that can then be used to satisfy wants and needs. Value in exchange means that value, that is satisfaction, is obtained indirectly through the acquisition of something else. For an item to have value in exchange it need NOT have value in use, value obtained directly from the consumption of a good or service.
Visit the GLOSS*arama
|
|


|

|
                           SAVING-INVESTMENT MODEL: A variation of the Keynesian injections-leakages model that includes the two private sectors, the household sector and the business sector. This variation, more formally termed the two-sector injections-leakages model, captures the interaction between induced saving (and indirectly induced consumption expenditures) and autonomous investment expenditures. This model provides an alternative to the two-sector aggregate expenditures (Keynesian cross) analysis of the macroeconomy, including equilibrium, disequilibrium, and the multiplier. Equilibrium is identified as the intersection between the saving line and the investment line. Two related variations are the three-sector injections-leakages model and the four-sector injections-leakages model. The saving-investment model provides an alternative to the more common two-sector Keynesian model; the Keynesian cross, aggregate expenditures-aggregate production model of the macroeconomy. Both models provide essentially the same analysis and are essentially "two sides of the same coin." The key difference between the two models is that consumption is explicitly eliminated from the injections-leakages variation. Whereas the Keynesian cross builds on the consumption function, the injections-leakages model builds on the saving function.Two SectorsThe two sectors included in this saving-investment model are the household sector and the business sector.- Household Sector: The household sector includes everyone in an economy who consumes goods and services. It is the entire population of an economy. The household sector is responsible for consumption expenditures on gross domestic product.
- Business Sector: The business sector contains the private, profit-seeking firms in the economy that combine scarce resources into the production of wants-and-needs satisfying goods and services. The business sector is responsible for investment expenditures on gross domestic product.
Injections and LeakagesOne half of the injections-leakages model is injections, which are non-consumption expenditures on aggregate production. The three injections are investment expenditures, government purchases, and exports. These are termed injections because they are "injected" into the core circular flow of consumption, production, and income. In the saving-investment model, investment expenditures are the only injection included.The other half of the injections-leakages model is leakages, which are non-consumption uses of the income generated from production. The three leakages are saving, taxes, and imports. These are termed leakages because they are "leaked" out of the core circular flow of consumption, production, and income. In the saving-investment model, saving is the only leakage included. Equilibrium in the injections-leakages model relies on a balance between the injections into the core circular flow and leakages out of the flow. If leakages match injections, then the volume of the core circular flow does not change. This is the same as achieving a balance between the water flowing from a faucet into a sink and that flowing out through the drain. When these two flows are equal, then the total amount of water IN the sink does not change. Equilibrium! In the saving-investment model, equilibrium is identified as a balance or equality between saving and investment expenditures. The Saving-Investment BalanceA balance between injections and leakages generates the same equilibrium as a balance between aggregate expenditures and aggregate production. A little manipulation of the Y = AE equilibrium condition illustrates why.- For the two-sector analysis, aggregate expenditures (AE) are the sum of consumption (C) and investment (I).
AE = C + I
- In the two-sector analysis, the income generated by aggregate production (Y) is used by the household sector for consumption (C) and saving (S).
Y = C + S
- Substituting each of these equations into the Y = AE equilibrium condition gives us:
C + S = C + I
- Because consumption (C) is on both sides, it cancels out.
S = I
This last equation indicates that equilibrium can be achieved by equating injections I with leakages S. Most importantly, when aggregate expenditures equal aggregate production (Y = AE), then injections are necessarily equal to leakages S = I. This results indicates why two-sector injections-leakages model is also termed the saving-investment model. This version of the injections-leakages model has its foundation in classical economics, particularly the key classical assumption that saving is equal to investment. The Graphical Model| The Injections-Leakages Model | 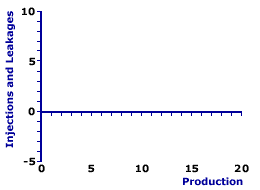 |
The exhibit to the right can be used to present the saving-investment model. As it currently stands, this exhibit is blank, except for the horizontal axis, which measures aggregate production, and the vertical axis, which measures the assorted injections. To move from this largely blank diagram we need to add leakages (saving) and injections (investment expenditures).A click of the [Leakages] button displays the leakages line, which is comprised exclusively of saving. The slope of this saving line is positive and equal to the marginal propensity to save. The vertical intercept of the saving line is negative, indicating that autonomous saving is negative. A click of the [Injections] button displays the injections line, which is based entirely on investment expenditures. To keep the analysis simple, investment expenditures are assumed to be autonomous, as indicated by the horizontal investment line. Induced investment would give the injections line a slight positive slope, but it would not affect the basic conclusions reached. With the saving and investment lines in place, the next step is to identify equilibrium. Because we are dealing only with two sectors -- household and business -- this injections-leakages model achieves equilibrium with equality between saving and investment. Equilibrium is found at the intersection of the saving line and the investment line. Click the [Equilibrium] button to highlight this point and the corresponding $12 trillion level of aggregate production. What key conclusions can be derived from this analysis. - First, saving is equal to investment, and leakages are equal to injections. As such, the total volume of the circular flow does not change.
- Second, if saving is not equal to investment, then the volume of the circular flow, especially aggregate production, changes. If saving exceeds investment, aggregate production declines. If investment exceeds saving, aggregate production rises.
- Third, the difference between saving and investment is unplanned inventory changes. If saving equals investment, then inventories don't change. If saving exceeds investment, inventories increase. If investment exceeds saving, inventories decrease.
Two Other VariationsThe saving-investment model (or two-sector injections-leakages model) is one of three variations, each based on a different combination of the four macroeconomic sectors, and thus a different number of injections and leakages.- Three-Sector Model: One variation of the injections-leakages model adds the government sector (or public sector) to the household and business sectors contained in the two-sector model. This variation is used to analyze government stabilization policies, especially how fiscal policy changes in government purchases and taxes can be used to close recessionary gaps and inflationary gaps. Saving and taxes are the two leakages. Investment and government purchases are the two injections.
- Four-Sector Model: As the name suggests, all four macroeconomic sectors--household, business, government, and foreign--are included in the four-sector model. This model is not only used to capture the interaction between the domestic economy and the foreign sector, but also provides the foundation for detailed, empirically estimated models of the macroeconomy. Saving, taxes, and imports are the three leakages. Investment, government purchases, and exports are the three injections.

Recommended Citation:SAVING-INVESTMENT MODEL, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2025. [Accessed: July 18, 2025].
Check Out These Related Terms... | | | | | | | | | |
Or For A Little Background... | | | | | | | | | | | | | | | | |
And For Further Study... | | | | | | | | | | | | |
Related Websites (Will Open in New Window)... | |
Search Again?
Back to the WEB*pedia
|



|

|
|
One of the largest markets for gold in the United States is the manufacturing of class rings.
|

|
|
"A winner is someone who recognizes his God-given talents, works his tail off to develop them into skills, and uses those skills to accomplish his goals. " -- Larry Bird, basketball player
|

|
BST
Bulk Supply Tariff
|

|
|
Tell us what you think about AmosWEB. Like what you see? Have suggestions for improvements? Let us know. Click the User Feedback link.
User Feedback
|


|


