The essence of the multiplier is that relatively small changes in autonomous expenditures or other shocks cause relatively large overall changes in aggregate production and income. The resulting changes in aggregate production are typically a "multiple" of the initial expenditure changes, hence the term "multiplier."The multiplier process works because a change in autonomous expenditures triggers a change in aggregate production, factor payments, and income, which then induces changes in other expenditures, especially consumption. These induced expenditures then cause further changes in aggregate production, factor payments, and income, when then induce further changes in expenditures. The process is cumulative and reinforcing.
Keynesian economics provides the ideal framework for analyzing the multiplier process and deriving specific multipliers. In particular, the cornerstone of the multiplier is induced consumption, as captured by the marginal propensity to consume, which is also a cornerstone of Keynesian economics.
A Graphical Shift
| An Expenditures Shift | 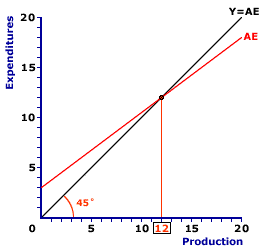
|
The multiplier process is commonly illustrated as a shift of the aggregate expenditures line in the Keynesian model. The exhibit to the right presents a standard Keynesian cross. The existing equilibrium is $12 trillion, given by the intersection of the aggregate expenditures line (AE) and the 45-degree line (Y = AE). This equilibrium, however, is about to change.Suppose, for example, that autonomous investment expenditures increase by $1 trillion, which is just the thing to shift the aggregate expenditures line and trigger the multiplier.
To display the shift of the aggregate expenditures line, click the [$1 Trillion More] button. This reveals a new aggregate expenditures line that is $1 trillion higher than the original line.
The new equilibrium is found at the intersection of the 45-degree line and the new aggregate expenditures line, which is $16 trillion of aggregate production. The difference between the original equilibrium and the new equilibrium is $4 trillion. This is four times the initial change in investment, which implies a multiplier of 4.
The Simple Expenditures Multiplier
THE multiplier is actually a set of multipliers that differ based on (1) the autonomous shock and (2) assumptions concerning what is induced by the changes in aggregate production and income. The simplest multiplier, which is often used to illustrate the basics of the multiplier process, is the simple expenditures multiplier.The simple expenditures multiplier is the ratio of the change in aggregate production to an autonomous change in an aggregate expenditure when consumption is the only induced expenditure. This simple expenditures multiplier is typically used to analyze shocks caused by changes in investment expenditures.
This simplest version of the simple expenditures multiplier comes from the two-sector Keynesian model that has nothing but induced consumption from the household sector and autonomous investment from the business sector. However, while this simple expenditures multiplier is derived from the basic two-sector Keynesian model, it works equally well for other models as long as consumption is the only induced expenditure.
This version is as simple as it gets while capturing the fundamentals of the multiplier. Autonomous investment triggers the multiplier process and induced consumption provides the cumulatively reinforcing interaction between consumption, aggregate production, factor payments, and income.
The formula for this simple expenditures multiplier, m, is:
Where MPC is the marginal propensity to consume and MPS is the marginal propensity to save.If, for example, the MPC is 0.75 (and the MPS is 0.25), then an autonomous $1 trillion change in investment expenditures results in a change in aggregate production of $4 trillion.
While the simple expenditures multiplier can be derived from the basic two-sector Keynesian multiplier, it also works for models with more sectors, as long as consumption is the only induced expenditure. If, for example, autonomous government purchases change by $1 trillion, then the change in aggregate production is $4 trillion, the same as with a $1 trillion change in investment expenditures. Moreover, the same change in aggregate production is realized if autonomous exports or consumption expenditures change by $1 trillion.
The Simple Tax Multiplier
A second multiplier, termed the tax multiplier, is used to analyze changes in government taxes. The tax multiplier is the ratio of the change in aggregate production to an autonomous change in taxes.The tax multiplier is extremely useful when it comes to analyzing fiscal policy changes in taxes. Tax reductions are an extremely popular application of expansionary fiscal policy when correcting a business-cycle contraction. A relatively small tax reduction, working through the multiplier process, can trigger a much larger change in aggregate production. The tax multiplier can be used to determine how much taxes need to be reduced to achieve full employment.
The key feature of the tax multiplier that differentiates it from the expenditures multiplier is how taxes affect aggregate expenditures. In particular, taxes do not affect aggregate expenditures directly (as do government purchases or investment). They affect aggregate expenditures indirectly through consumption.
A change in taxes means the household sector has a change in disposable income. The household sector then reacts to this change in disposable income by changing both consumption and saving. How much consumption changes is based on the marginal propensity to consume.
With these thoughts in mind, let's look at the specification for the simple tax multiplier (m[tax]).
| m[tax] | = | - MPC | x | 1
MPS | = | - MPC
MPS |
Where MPC is again the marginal propensity to consume and MPS is the marginal propensity to save.This formula is almost identical to that for the simple expenditures multiplier. The only difference is the inclusion of the negative marginal propensity to consume (- MPC).
The MPC means that for each one dollar change in taxes, consumption and thus aggregate expenditures change by only a fraction. The fraction is equal to the MPC.
The MPC is negative because an increase in taxes decreases income, consumption, and thus aggregate expenditures, and a decrease in taxes increases income, consumption, and aggregate expenditures.
Suppose, for example, that the government sector reduces taxes by $1 trillion with the goal of stimulating aggregate production and warding off a business-cycle contraction. This tax reduction increases household income by $1 trillion. The household sector spends part and saves part of this income. The division between consumption and saving is based on the marginal propensities to consume and save.
If the marginal propensity to consume is 0.75, then consumption increases by $750 billion. This $750 billion change in consumption then triggers the multiplier process much like that seen for the investment injection. The difference, however, is the full $1 trillion change in investment triggers the multiplier process, but only 75% of the change in taxes works its way into the multiplier.
The Balanced-Budget Multiplier
Another interesting multiplier is the combination of two multipliers -- the simple expenditures multiplier and the tax multiplier. More specifically it is the simple expenditures multiplier for government purchases combined with the tax multiplier. This is termed the balanced-budget multiplier.The logic behind this multiplier comes from the government's budget, which includes spending and taxes. In general, a balanced budget has an equality between spending and taxes. As such, the balanced-budget multiplier analyzes what happens when there is an equality between changes in government purchases and taxes.
The balanced-budget multiplier is the ratio of the change in aggregate production to an autonomous change in government purchases, which are matched by an equal change in taxes.
In other words, the balanced-budget multiplier indicates the overall impact on aggregate production of a change in government purchases that is matched (that is, paid for) by an equivalent change in taxes. The balanced-budget multiplier, as such, is actually the sum of the simple expenditures multiplier (for government purchases) and the tax multiplier.
Here is the balanced-budget multiplier (m[bb]).
| m[bb] | = | 1
MPS | + | - MPC
MPS | = | 1- MPC
MPS | = | MPS
MPS | = | 1 |
The most obvious and most important conclusion is that the balanced-budget multiplier has a value of 1. Suppose, for example, that government purchases are increased by $1 trillion as a fiscal policy move to correct a business-cycle contraction. By itself, this $1 trillion government purchases increase would be expected to trigger a $4 trillion increase in aggregate production. Presumably this is the amount needed to achieve full employment.
If, however, this $1 trillion increase in government purchases is matched by, and paid for with, an equal $1 trillion increase in taxes, then the net impact on aggregate production is only $1 trillion, not $4 trillion. If a $4 trillion increase in aggregate production is needed to achieve full employment, then this strategy falls $3 trillion short.
This occurs because only the initial $1 trillion government purchase triggers an increase in aggregate production. Each subsequent round of increased consumption is offset by decreased consumption caused by higher taxes. The only expenditure that does not go through the household sector and is not cancelled by taxes is the original government purchase.
More Complex Multipliers
The three multipliers discussed thus far have all been variations on a theme. The theme is a simple Keynesian model in which consumption is the only induced component. Differences between the simple expenditures multiplier, the tax multiplier, and the balanced-budget multiplier are based on autonomous shocks that trigger the multiplier, not the induced components of the model.In the real world, however, consumption is not the only induced expenditure. Investment, government purchases, taxes, and net exports (through imports) are also induced. What we need is a more complex multiplier in which other induced components are included.
Here is the formula for just such a multiplier, which can be labeled m[all].
| m[all] | = | 1
{1 - [MPC + MPI + MPG - (MPC x MPT) - MPM]} |
This particular multiplier has a number of abbreviations containing the letters "MP." These are the assorted induced components, with "MP" standing for marginal propensity. In fact, the batch of abbreviations within the brackets "[]" is actually the slope of the aggregate expenditures line.Let's run through the cast of characters in this formula.
This complex expenditures multiplier can be used to determine the change in aggregate production resulting from a change in any autonomous expenditure, including consumption, investment, government purchases, and net exports.A complex tax multiplier looks very similar, but includes an adjustment for the marginal propensity to consume portion of a tax change that affects aggregate expenditures. The formula for the complex tax multiplier m[tax-all] is:
| m[tax-all] | = | - MPC
{1 - [MPC + MPI + MPG - (MPC x MPT) - MPM]} |
MULTIPLIER, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2025. [Accessed: June 30, 2025].


