
|
|
EUROPEAN UNION: The economical and political integration of a dozen European nations created by the Maastricht Treaty signed in 1992. The twelve nations forming the European Union (commonly abbreviated EU) are Belgium, Denmark, Greece, Germany, Spain, France, Ireland, Italy, Luxembourg, Netherlands, Portugal, and Great Britain. Three additional nations that have joined the original dozen are Austria, Finland and Sweden. The Economic Union was actually one of several steps by European nations after the end of World War II to promote integration. This Economic Union was established to reduce or eliminate many tariffs and nontariff barriers, create a single monetary unit (the euro), establish of a common military and defense policy, and centralize monetary policy.
Visit the GLOSS*arama
|
|


|

|
                           LAW OF DEMAND: The inverse relationship between demand price and the quantity demanded, assuming ceteris paribus factors are held constant. This fundamental economic principle indicates that a decrease the price of a commodity results in an increase in the quantity of the commodity that buyers are willing and able to purchase in a given period of time, if other factors are held constant. The law of demand is one of the most important principles found in the study of economics. The law of demand is the scientific relation between demand price and quantity demanded that captures the demand side of the market. When combined with the law of supply (or other relevant supply principles) the result is the market model. The market provides a powerful tool for analyzing exchanges, resource allocation, and efficiency. What Does It Mean?The inverse relation of this law means that buyers are willing and able to buy more of a good if the price is lower and less of a good if the price is higher. From a scientific method perspective, this indicates that price causes quantity demanded. Or more specifically that a change in the demand price causes a change in the quantity demanded.Working the Curve| Demand Curve | 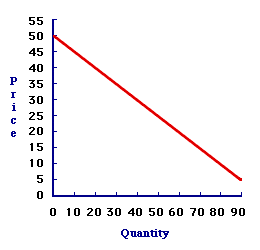 |
The law of demand is conveniently illustrated by a demand curve. In particular, it is illustrated by the negative slope of a demand curve, such as the one presented to the right. The negative slope of the demand curve means that higher prices are related to smaller quantities and that lower prices are related to larger quantities. Price goes up, quantity goes down. Price goes down, quantity goes up.Two EffectsAn initial look into why the law of demand exists reveals two effects--income effect and substitution effect.- Income Effect: This is the observation that a change in the price of a good alters the purchasing power of income. If the price increases, then buyers are able to buy a smaller quantity with available income. If the price decreases, then buyers are able to buy a larger quantity with available income. A change in price induces an inverse, or opposite, change in the quantity demanded.
- Substitution Effect: This is the observation that a change in the price of a good alters the relative prices of substitute goods, which then motivates buyers to buy more or less of the substitute goods, and less or more of this good. If the price increases, then the price of substitute goods become relatively lower, inducing buyers to buy more of those goods and a smaller quantity of this good. If the price decreases, then the price of substitute goods become relatively higher, inducing buyers to buy less of those goods and a larger quantity of this good. A change in price induces an inverse, or opposite, change in the quantity demanded.
Looking Into UtilityFurther support of the law of demand is provided by the analysis of utility and consumer demand theory. The inverse relation between demand price and quantity demanded can be tentatively explained through two related notions of consumer behavior.- Diminishing Marginal Utility: This notion states that the extra satisfaction obtained from a good declines as larger amounts are consumed. If buyers receive less satisfaction, then they are willing to pay a lower price, which generates the law of demand. The downside of this explanation is the inability to measure the actual utility derived from consuming a good.
- Decreasing Marginal Rate of Substitution: The notion states that the relative satisfaction obtained from a good declines as larger amounts are consumed (and smaller amounts of other goods are consumed). In this case, if buyers receive relatively less satisfaction, then they are willing to pay a relatively lower price. The law of demand is implied by this analysis by using the ceteris paribus assumption that other factors (including other prices) remain unchanged. The advantage of this explanation is that only a ranking of preferences is needed. There is no need to actually measure utility.
An ExceptionWhile the law of demand is a well-documented, extensively tested economic principle, it is not without exception. That exception is termed a Giffen good. A Giffen good is one in which a change in price causes quantity to change in the same direction. An increase in price causes an increase in quantity and a decrease in price causes a decrease in quantity.A Giffen good exists because the good in question is an inferior good (an increase in income causes a decrease in demand) and the income effect overwhelms the substitution effect. Giffen goods are extremely rare and generally only surface if buyers spend a substantial portion of their income on an inferior good.

Recommended Citation:LAW OF DEMAND, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2025. [Accessed: July 18, 2025].
Check Out These Related Terms... | | | | | | | | |
Or For A Little Background... | | | | | | | | | | | | | | |
And For Further Study... | | | | | | | | | | | | | | | | | | | |
Search Again?
Back to the WEB*pedia
|



|

|
WHITE GULLIBON
[What's This?]
Today, you are likely to spend a great deal of time searching the newspaper want ads seeking to buy either an extra large beach blanket or a large flower pot shaped like a Greek urn. Be on the lookout for fairy dust that tastes like salt.
Your Complete Scope
This isn't me! What am I?
|

|
|
Sixty percent of big-firm executives said the cover letter is as important or more important than the resume itself when you're looking for a new job
|

|
|
"A winner is someone who recognizes his God-given talents, works his tail off to develop them into skills, and uses those skills to accomplish his goals. " -- Larry Bird, basketball player
|

|
AOM
Australian Options Market
|

|
|
Tell us what you think about AmosWEB. Like what you see? Have suggestions for improvements? Let us know. Click the User Feedback link.
User Feedback
|


|


