Comparable to any profit-maximizing firm, a perfectly competitive firm produces the quantity of output in the short run that generates the maximum difference between total revenue with total cost, which is economic profit. This profit maximizing level of production is also achieved by the equality between marginal revenue and marginal cost. At this production level, the firm cannot increase profit by changing the level of production. The analysis of marginal revenue and marginal cost can be achieved through a table of numbers or with marginal revenue and marginal cost curves.

Working the Numbers

Because the zucchinis Phil produces are identical to those produced by gadzillions of other zucchini growers, he has no market control and must sell his zucchinis at the going market price of $4 per pound. Phil is a price taker. Phil's status as a perfectly competitive, price-taking firm is reflected in this table.

The Zucchini Numbers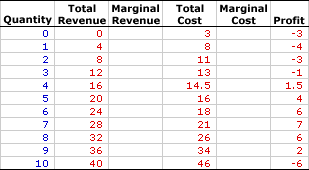

• Quantity: The first column presents the quantity of output produced, ranging from 0 to 10 pounds of zucchinis.


• Total Revenue: The second column presents total revenue, ranging from a low of $0 for no output to a high or $40 for 10 pounds of zucchinis. If Phil sells 1 pound of zucchinis, he receives $4 in total revenue. Total revenue is $8 for 2 pounds of zucchinis. The total revenue in the second column is the $4 market price times the quantity of zucchinis sold.


• Total Cost: The fourth column presents the total cost incurred by the firm in the production of this output, ranging from a low of $3 for zero output to a high of $46 for 10 pounds of zucchinis. Because Phil has fixed cost, he incurs $3 of total cost even though he produces no zucchinis. Producing 1 pound of zucchinis incurs a total cost of $8. Producing 2 pounds of zucchinis incurs a total cost of $11. Total cost rises as Phil produces more.


• Profit: The sixth column at the far right of the table is profit, the difference between total revenue in the second column and total cost in the fourth column. It begins at -$3, falls to -$4, rises to $7, then falls to -$6.

1. Marginal revenue indicates how much total revenue changes by producing one more or one less unit of output.
2. Marginal cost indicates how much total cost changes by producing one more or one less unit of output.
3. Profit increases if marginal revenue is greater than marginal cost and profit decreases if marginal revenue is less than marginal cost.
4. Profit neither increases nor decreases if marginal revenue is equal to marginal cost.
5. As such, the production level that equates marginal revenue and marginal cost is profit maximization.

• Marginal Revenue: Marginal revenue in the third column is a constant at the $4 per pound for every quantity of output. Marginal revenue is constant and equal to price because Phil is a perfectly competitive firm. The price is fixed and so too is marginal revenue.


• Marginal Cost: Marginal cost in the fifth column starts at $5, declines to a low of $1.50, the rises again to $12. The declining values are the result of increasing marginal returns and the rising values are due to decreasing marginal returns and the law of diminishing marginal returns.

• First, a quick look at the profit column indicates that the profit-maximizing production is 7 pounds of zucchinis, which generates a profit of $7. Click the [Profit Max] button to highlight this result.


• Second, with this outcome highlighted, note the corresponding marginal revenue and marginal cost values. Marginal revenue is $4 for the seventh pound of zucchini production and marginal cost is $3.

  Phil increases production from 6 pounds to 7 pounds because doing so generates $4 of extra revenue and incurs only $3 of extra cost, meaning his profit increases by $1 over the production of 6 pounds. Phil does not increase production from 7 pounds to 8 pounds because doing so generates only $4 of extra revenue but incurs $5 of extra cost, meaning his profit decreases by $1.

  As such, Phil settles in with the production and 7 pounds of zucchinis and achieves maximum profit. He cannot increase profit by changing production.



• Third, while marginal revenue and marginal cost might not appear to be equal for this profit-maximizing 7 pounds of zucchini production ($4 versus $3), they really are. The reason is that the marginal numbers in the table actually represent discrete changes from one pound to the next. Reducing the size of the discrete change, say from 6.9999 pounds to 7 pounds, actually results in a marginal cost that is closer to $4. At the limit of an infinitesimally small change, marginal cost is exactly $4 and equal to marginal revenue.

  While the equality between marginal revenue and marginal cost shows up better in a graph, the best practical method of identifying similar results using a table of numbers such as this one, is to average the discrete changes on either side of the quantity. For example, the marginal cost AT the seventh pound of zucchini production is the average of the change from 6 to 7 ($3) and from 7 to 8 ($5), which is $4.

Working the Curves

The Zucchini Curves

• Marginal Revenue: A click of the [Marginal Revenue] button reveals a horizontal, perfectly elastic green line labeled MR that depicts the marginal revenue Phil receives from zucchini production. The line is horizontal at the constant value of $4.


• Marginal Cost: A click of the [Marginal Cost] button reveals a red U-shaped curve labeled TC that represents the marginal cost Phil incurs in the production of zucchinis. The shape is based on increasing, then decreasing marginal returns.

To demonstrate why the equality between marginal revenue and marginal cost is the profit-maximizing production level, consider what results if marginal revenue is not equal to marginal cost:

• If marginal revenue is greater than marginal cost, as is the case for small quantities of output, then the firm can increase profit by increasing production. Extra production adds more to revenue than to cost, so profit increases.


• If marginal revenue is less than marginal cost, as is the case for large quantities of output, then the firm can increase profit by decreasing production. Reducing production reduces revenue less than to it reduces cost, so profit increases.


• If marginal revenue is equal to marginal cost, then the firm cannot increase profit by producing more or less output. Profit is maximized.