|
|
DIAMOND-WATER PARADOX: The perplexing observation that water, which is more useful than diamonds, has a lower price. If price is related to utility, how can this occur? This paradox was first proposed by classical economists in the 19th century and was subsequently used as a stepping stone for developing the notion of marginal utility and the role it plays in the demand price of a good. The paradox is magically cleared up with an understanding of marginal utility and total utility. People are willing to pay a higher price for goods with greater marginal utility. As such, water which is plentiful has enormous total utility, but a low price because of a low marginal utility. Diamonds, however, have less total utility because they are less plentiful, but a high price because of a high marginal utility.
Visit the GLOSS*arama
|
|
|
|
                           TOTAL PRODUCT AND AVERAGE PRODUCT: A graphical connection between the total product curve and the average product curve stating that the slope of a line between the origin and any point on the total product curve is equal to the average product. Imagine a ray shooting from the origin and hitting the total product curve. As this ray hits each point on the curve, remaining anchored at the origin, the slope of the ray changes, and the slope of this ray is average product. What is the logic behind this total-average relation? The slope of any line is the rise over the run, in this case the change in total product divided by the change in variable input. This, by the way, is the verbal description of marginal product. However, because the line is anchored at the origin, any changes in total product and variable input are changes from zero. In other words, the "change in" calculations are not incremental changes, but rather the total values up to that point of production--total product and the total quantity of the variable input used to produce the total product. This is simply the calculation of average product. Making Tacos| Total and Average Product |  |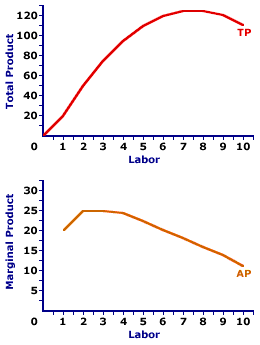
A graph should help illustrate the relation between total product and average product. The graph to the right is the hourly production of Super Deluxe TexMex Gargantuan Tacos (with sour cream and jalapeno peppers). The top panel of the graph is the total product curve. The bottom panel is the average product curve.For the relation between these two curves, a few buttons need to be clicked. - After clicking the [A] button, a line connecting the origin with a point on the total product curve is revealed. This point is a total product of 120 Gargantuan Tacos resulting from employing 6 workers. The slope of this line is equal to 10 tacos per worker. This corresponds exactly with the average product of 10 tacos per worker.
- Clicking the [B] button displays a second line connecting the origin with a total product/variable input quantity of 125 Gargantuan Tacos and 8 workers. The slope of this line is equal to 15.83 tacos per worker, which exactly to the average product of 15.83 tacos per worker.
- Clicking the [C] button displays a third line connecting the origin with a total product/variable input quantity of 110 Gargantuan Tacos and 10 workers. The slope of this line is equal to 11 tacos per worker, which is exactly to the average product of 11 tacos per worker.
Marginal and AverageOne additional button that needs to be clicked is the one labeled [Marginal]. This button displays a relatively important line. Because this line connects the origin and the total product curve, like the other lines presented here, the slope measures average product. However, this line is also tangent to the total product curve. As a tangent, the slope of this line is also the slope of the curve at the point of tangency. But the slope of the total product curve is marginal product.What does this mean? It means that this particular line measures both average product and marginal product. It means that at 2.5 workers, marginal product and average product are exactly the same.
Recommended Citation:TOTAL PRODUCT AND AVERAGE PRODUCT, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2024. [Accessed: December 7, 2024].
Check Out These Related Terms... | | | |
Or For A Little Background... | | | | | | | |
And For Further Study... | | | | | | | | | | |
Search Again?
Back to the WEB*pedia
|
|
|
YELLOW CHIPPEROON
[What's This?]
Today, you are likely to spend a great deal of time strolling around a discount warehouse buying club trying to buy either decorative celebrity figurines or a flower arrangement with anything but tulips for your grandfather. Be on the lookout for defective microphones.
Your Complete Scope
This isn't me! What am I?
|
|
|
Cyrus McCormick not only invented the reaper for harvesting grain, he also invented the installment payment for selling his reaper.
|
|
|
"If you don't know where you are going, any road will get you there." -- Lewis Carroll, writer
|
|
AASB
American Assocation of Small Business
|
|
|
Tell us what you think about AmosWEB. Like what you see? Have suggestions for improvements? Let us know. Click the User Feedback link.
User Feedback
|
|
