
|
|
GOODS: When used without an adjective modifier (like "final" goods or "intermediate" goods), this generically means physical, tangible products used to satisfy people's wants and needs. This term good should be contrasted with the term services, which captures the intangible satisfaction of wants and needs. As such, you will frequently see the plural combination of these two phrases together "goods and services" to indicate the wide assortment of economic goods produced using the economy's scarce resources. As you might imagine this general notion of wants and needs satisfying goods and services pops up throughout the study of economics.
Visit the GLOSS*arama
|
|


|

|
                           PERFECT COMPETITION, LOSS MINIMIZATION: A perfectly competitive firm is presumed to produce the quantity of output that minimizes economic losses, if price is greater than average variable cost but less than average total cost. This is one of three short-run production alternatives facing a firm. The other two are profit maximization (if price exceeds average total cost) and shutdown (if price is less than average variable cost). A perfectly competitive firm guided by the pursuit of profit is inclined to produce the quantity of output that equates marginal revenue and marginal cost in the short run, even if it is incurring an economic loss. The key to this loss minimization production decision is a comparison of the loss incurred from producing with the loss incurred from not producing. If price exceeds average variable cost, then the firm incurs a smaller loss by producing than by not producing.One of Three Alternatives| Production Alternatives | | Price and Cost | Result |
|---|
| P > ATC | Profit Maximization | | ATC > P > AVC | Loss Minimization | | P < AVC | Shutdown |
Loss minimization is one of three short-run production alternatives facing a perfectly competitive firm. All three are displayed in the table to the right. The other two are profit maximization and shutdown.- With profit maximization, price exceeds average total cost at the quantity that equates marginal revenue and marginal cost. In this case, the firm generates an economic profit.
- With shutdown, price is less than average variable cost at the quantity that equates marginal revenue and marginal cost. In this case, the firm incurs a smaller loss by producing no output and incurring a loss equal to total fixed cost.
Zucchini ProductionThe marginal approach to analyzing a perfectly competitive firm's short-run production decision can be used to identify the economic loss alternative. The exhibit displayed here illustrates the short-run production decision by Phil the perfectly competitive zucchini grower. | Incurring a Loss | 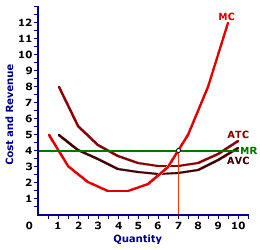 |
The three U-shaped cost curves used in this analysis provide all of the information needed on the cost side of the firm's decision. The demand curve facing the firm (which is also the firm's average revenue and marginal revenue curves) provides all of he information needed on the revenue side.For the time being, Phil faces a $4 price for his zucchinis. As such he produces 7 pounds of zucchinis, which equates the $4 marginal revenue with marginal cost. However, should this price decline, say to $2.60 per pound, then maximizing a positive profit is not his primary concern. His decision turns to minimizing losses. Click the [$2.60] button to illustrate the situation facing Phil with a lower price. The key to this lower price is that it intersects the marginal cost curve between the average total cost curve and the average variable cost curve. This is crucial. It means that Phil does not generate enough revenue per pound of zucchinis sold (average revenue = $2.60) to cover the cost of producing each pound of zucchinis (average total cost = $3). Phil clearly incurs an economic loss on each pound of zucchinis produced and sold. In fact, if Phil produces 6.25 pounds of zucchinis (the quantity that equates marginal revenue and marginal cost), then his total cost is $18.75, but his total revenue is only $16.25. He incurs an economic loss of $2.50, a loss of $0.40 per pound produced. The Short-Run ChoicePerhaps Phil should stop producing. Perhaps he would be better off by NOT selling zucchinis. Unfortunately, Phil is faced with short-run fixed cost. Phil incurs a total fixed cost of $3 whether or not he engages in any short-run production. Even if he shuts down production, he still must pay this $3 of fixed cost.As such, Phil is faced with a comparison between the loss incurred from producing with the loss incurred from not producing. Those are his two short-run choices. If he produces, he incurs a loss of $2.50. If he does not produce, he incurs a loss of $3. The choice seems relatively obvious: Phil is better to produce 6.25 pounds of zucchinis, incurring an economic loss of $2.50, and hoping for an increase in the price. Phil continues to produce in the short run because he generates enough revenue to pay ALL of his variable cost, plus a portion of his fixed cost. By producing 6.25 pounds of zucchinis, he generates $16.25 of total revenue. While this revenue falls short of covering the $18.75 of total cost entirely, it is enough to pay the $15.75 of total variable cost, with an extra $0.50 left over to pay a portion of the $3 total fixed cost. This is why the economic loss from production is less than total fixed cost. Because Phil has no market control, he is subject to the whims of the market price. This $2.60 zucchini price generates sufficient total revenue for Phil to pay ALL variable cost and some fixed cost. However, should this market price drop, then Phil would have to reevaluate his production decision. If the price declines enough, Phil will be forced to shut down production in the short run.

Recommended Citation:PERFECT COMPETITION, LOSS MINIMIZATION, AmosWEB Encyclonomic WEB*pedia, http://www.AmosWEB.com, AmosWEB LLC, 2000-2025. [Accessed: July 18, 2025].
Check Out These Related Terms... | | | | | |
Or For A Little Background... | | | | | | | | | | | |
And For Further Study... | | | | | | | | |
Search Again?
Back to the WEB*pedia
|



|

|
BROWN PRAGMATOX
[What's This?]
Today, you are likely to spend a great deal of time browsing through a long list of dot com websites seeking to buy either a case of blank recordable DVDs or a pair of red goulashes with shiny buckles. Be on the lookout for mail order catalogs with hidden messages.
Your Complete Scope
This isn't me! What am I?
|

|
|
Potato chips were invented in 1853 by a irritated chef repeatedly seeking to appease the hard to please Cornelius Vanderbilt who demanded french fried potatoes that were thinner and crisper than normal.
|

|
|
"A winner is someone who recognizes his God-given talents, works his tail off to develop them into skills, and uses those skills to accomplish his goals. " -- Larry Bird, basketball player
|

|
ICSID
International Center for the Settlement of Investment Disputes
|

|
|
Tell us what you think about AmosWEB. Like what you see? Have suggestions for improvements? Let us know. Click the User Feedback link.
User Feedback
|


|


