Because a risk loving person obtains more utility from risky income than from certain income, it follows that a larger amount of certain income generates the same utility as the risky income. This means that a risk loving person is actually willing to pay to undertake risk. This difference in income is termed the risk premium and is the maximum price that a risk loving person would pay for the opportunity to engage in risk.

Two other risk preferences are risk aversion and risk neutrality. A risk averse person has decreasing marginal utility of income and prefers certain income to risky income. A risk neutral person has constant marginal utility of income and prefers risky income and certain income equally.

Marginal Utility of Income

Marginal Utility of 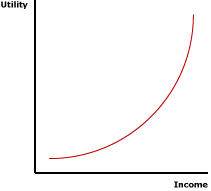Income

The standard view in consumer demand theory is that the marginal utility of income decreases with an increase in the quantity consumed. This gives justification for the negatively-sloped demand curve. This view also generally applies to the marginal utility of income. An increase in income results in a decrease in marginal utility.

However, the analysis of risk preferences indicates the possibility of increasing marginal utility of income. In this case an increase in income results in a increase in marginal utility. Increasing marginal utility of income results in risk loving. However, the marginal utility of income can also remain constant, leading to risk neutrality.

The exhibit to the right presents increasing marginal utility of income. At low levels of income, the curve is relatively flat, then grows steeper at higher income levels. A curve of this shape is commonly termed convex. It indicates that the change in marginal utility begins relatively low, then increases as income increases.

Increasing marginal utility of income, represented by a convex curve, is the key to risk loving. Decreasing and constant marginal utility of income, represented by a concave curve and a straight line, give rise to risk aversion and risk neutrality, respectively.

Risk or Certainty?

• Certain Income: This is income obtained with absolutely certainty. There is no risk involved. In this analysis of risk loving, certain income can be thought of as the amount of income that a person has without engaging in a risky situation or wager. There is no chance of receiving any more income or any less income.


• Risky Income: This is income based on the results of a risky situation, such as a wager. The risky situation might result in more income or less income. The amount of risky income is specified as the expected value, a balance between the probability of the lost income and the probability of gained income.

The $100 that Winston has at the start, and would keep if he did not wager, is the certain income. If he wants to keep this $100, then he can walk away from the wager.

The risky income is the amount of income that he can expect to have after the wager. It's not $50 or $150, but the average of the two, $100, weighted by the probability of winning or losing. In other words, the expected income of a 50-50 wager is the amount of income he would expect to end up with after undertaking the wager a number of times, say a 100 or more. If he undertakes this wager 100 times, he can expect to win $50 exactly half of the time and lose $50 exactly half of the time. The loses exactly balance the wins and the income he can expect to end up with is $100.

This can be summarized with the following equation.

Expected Income

=

[(p) x income with loss]

+

[(1-p) x income with win]

Expected Income

=

[(0.5) x $50]

+

[(0.5) x $150]

Expected Income

=

$100

The Utility of Income

• Utility of Expected Income: This is simply the amount of utility generated by income. It is identified by a utility curve such as presented in the above exhibit. It is the utility generated by certain income. Or it is the utility associated with expected income. In the previous coin-flip example facing Winston Smythe Kennsington III, the utility of certain income is equal to the utility of income expected.


• Expected Utility: This is the average utility expected from a risky situation. Like expected income, it is the utility obtained with a loss, weighted by the probability of losing, plus the utility obtained with a win, weighted by the probability of win.

In contrast, expected utility is identified by separately calculating the income from a loss, and the corresponding and the income from a win, then determining the utility from each. These utility values are then averaged, weighted by the probability of a loss and a win.

Expected Utility

=

[(p) x utility from income with loss]

+

[(1-p) x utility from income with gain]

Working Through a Graph

Risk Loving

Let's re-evaluate the $50 flip-of-a-coin wager facing Winston Smythe Kennsington III.

• First: Take note of $100 of certain income that Winston has before the wager. Click the [Certain Income] button to identify this amount. Also note the amount of utility generated by this $100 of certain income, measured as U(100) on the vertical axis.


• Second: Now consider the wager, with a 50-50 chance of Winston winning or losing $50. Click the [Risky Income] button to identify the possible results. If Winston loses, he ends up with $50. If he wins, he ends up with $150. Also note that the expected income for this wager is $100, which like certain income generates U(100) utility, as well.


• Third: Next up is calculating expected utility from the wager. This is accomplished by identifying the utility generated by each separate outcome of the wager. Click the [Expected Utility] button for this information. The utility generated by the income resulting from the loss is measured as U(50) and the utility generated by the income resulting from the win is measured as U(150). Expected utility is then the weighted average of these two values, weighted by the probabilities of winning and losing. It is the seen as the utility associated with the intersection of the $100 of income and a straight line connecting the two utility/income wager possibilities and is measured as EU(100).

However, another important implication can also be had, the risk premium. This is the amount that Winston would be willing to pay to engage in risk. It can be identified by noting the amount of income that would generate the same utility as the expected utility of the wager. A click of the [Risk Premium] button reveals this information. Note that $118 of income generates the same utility, U(118), as the expected utility from the wager EU(100).

The difference between these two income levels $100 and $118, is the risk premium. That is, Winston is willing to pay up to $25 for the opportunity to undertake wager, to engage in risk.

Other Risk Preferences

• Risk Aversion: Risk aversion occurs when a person prefers certain income over risky income and arises due to decreasing marginal utility of income. A person with decreasing marginal utility of income obtains less utility from the income won than the income lost. The utility from winning is exceeded by the utility from losing. Even though the expected income is equal to the certain income, the utility obtained from the certain income is greater than of the utility obtained from the expected income. A risk aversion person is better off not wagering.


• Risk Neutrality: Risk neutrality occurs when a person prefers risky income equally to certain income and arises due to constant marginal utility of income. A person with constant marginal utility of income obtains the same utility from the income won as the income lost. The utility from winning equals the utility from losing. Not only is the expected income equal to the certain income, the utility obtained from the certain income equals the utility obtained from the expected income. A risk neutral person is indifferent about wagering.